ドラ枚数の分布（続き）

ドラが一枚も含まれていない確率を求めたのと同様の計算式によって、一枚の場合、二枚の場合…の確率を計算すると以下のようになります。

1枚の確率

₁₃₂C₁₂ * ₄C₁ / ₁₃₆C₁₃

132・131 ... 122・121 / 12・11 ... 2・1

136・135 ... 125・124 / 13・12 ... 2・1

13 ・ (123・122・121 / 136・135・134・133) ・ 4 = 0.2886

₁₃₂C₁₁ * ₄C₂ / ₁₃₆C₁₃

132・131 ... 123・122 / 11・10 ... 2・1

136・135 ... 125・124 / 13・12 ... 2・1

13 ・ 12 ・ (123・122 / 136・135・134・133) ・ 6 = 0.0429

₁₃₂C₁₀ * ₄C₃ / ₁₃₆C₁₃

132・131 ... 124・123 / 10・9 ... 2・1

136・135 ... 125・124 / 13・12 ... 2・1

13 ・ 12 ・ 11 ・ (123 / 136・135・134・133) ・ 4 = 0.0026

₁₃₂C₉ * ₄C₄ / ₁₃₆C₁₃

132・131 ... 125・124 / 9・8 ... 2・1

136・135 ... 125・124 / 13・12 ... 2・1

13 ・ 12 ・ 11 ・ 10 ・ ( 1 / 136・135・134・133) ・ 1 = 0.000052

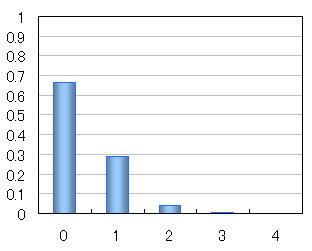
上記で得られた結果を棒グラフにしたものを示します。

三回に二回はドラが一枚も入っていないことになります。一枚だけ含まれる確率は30%弱、二枚の確率は4%ちょっとです。暗刻で入っている確率は0.26%、四枚とも持ってくる確率は0.005%です。

これを見る限り、配牌に一枚もドラがないからといって、別に悲観する必要はないということになります。